倒立制御解説(センシング準備編)
前回、倒立制御向けのハードウェア選定を行いました。
今回はセンシングの下準備をします。
センサの生値そのままでも制御ができますが、下ごしらえしておくことで後の作業が楽になります。
関連:
・ハード選定
・諸元測定
・制御方法基礎
接続設定はマイコンごとに異なるので割愛しますが、
・PWM出力
・エンコーダ用パルス入力
・ジャイロ兼加速度センサー接続
・float型演算(三角関数演算)
の準備ができたものとします。
また、実行周期を安定化させるために
・システム時刻を取得する機能
も準備してください。
実行周期は20ms周期であれば立つことを確認しています。
sample_time_ms = 20;
sample_time_s = sample_time_ms/1000.0f;
そこで、向きを定義します。

今回はセンシングの下準備をします。
センサの生値そのままでも制御ができますが、下ごしらえしておくことで後の作業が楽になります。
関連:
・ハード選定
・諸元測定
・制御方法基礎
接続設定はマイコンごとに異なるので割愛しますが、
・PWM出力
・エンコーダ用パルス入力
・ジャイロ兼加速度センサー接続
・float型演算(三角関数演算)
の準備ができたものとします。
また、実行周期を安定化させるために
・システム時刻を取得する機能
も準備してください。
実行周期は20ms周期であれば立つことを確認しています。
sample_time_ms = 20;
sample_time_s = sample_time_ms/1000.0f;
向きを定義する
向きや進行方向をそれぞれ適当に決めると後で整合性がとれなくなります。そこで、向きを定義します。
表裏
マイコン等が搭載された側を表(上)とします。
前後
地面に寝かせた状態でタイヤのある側を後ろとします。
表裏と前後を決めれば左右が決まります。
角度
表面を上にして寝かせた状態を0度とします。
ここから立たせる側を正とします。
構造によりますが、立った状態でほぼ+90度となります。
そこで、ジャイロ(角速度)と加速度から傾斜角度を計算します。
既存のライブラリーで手軽に済ますならMadgwickフィルターを使うのが良いでしょう。
今回はどんな環境でも実行できるようになるべく原理レベルからプログラムも自作します。
クォータニオン等を使って姿勢計算するのがベストですが、とりあえず1軸だけ計算しておけばOKです。
カルマンフィルタを使う方が良いとかありますが、通信式ジャイロで倒立制御を行う分にはそこまで気にする必要はありません。今回は簡易的な相補フィルタで対応します。
とりあえずジャイロと加速度の生値を取得します。
ジャイロの感度は1000deg/s以上、できれば2000deg/sに設定します。
感度の調整方法とデータの取得方法は使用するジャイロのマニュアルに従ってください。
ジャイロと加速度の生値(raw)は以下に格納するとします。
gyr_x_raw,gyr_y_raw,gyr_z_raw
acc_x,acc_y,acc_z
この時点でどの軸がどっちを向いているか確認しておいてください。
どの軸がどっちを向いているかはセンサを取り付けた向きで異なります。
M5StickCを使ったテスト用の構成の場合

水平状態で加速度Zがプラス
垂直状態で加速度Xがマイナス
水平から垂直に動かすとジャイロYがプラス
となりました。
以降はこれを基準に説明します。
ジャイロの値は静止状態で0が出力されてない事があるので、
起動数秒間の値を平均してゼロ点として使います。
平均化の例
gyr_x_zero = gyr_x_zero*0.99f + gyr_x_raw*0.01f;
gyr_y_zero = gyr_y_zero*0.99f + gyr_y_raw*0.01f;
gyr_z_zero = gyr_z_zero*0.99f + gyr_z_raw*0.01f;
この例では1周期ごとに1%ずつ値が更新されます。
私はジャイロの変動量を見て、静止状態が1秒以上続いたら平均値としています。
生値からゼロ点を引いて現在値とします。
取得したジャイロの値がdeg/s等の場合はrad/sへ換算しておきます。
また、回転方向の定義とジャイロの向きが一致するように補正します。
今回は起こすとジャイロYがプラスなので
gyr_rad = +(gyr_y_raw - gyr_y_zero)/180.0f*PI;
となります。
ゼロ点補正したジャイロの値を実行周期毎に積算(数値積分)すれば角度になります。
現在のジャイロ角度rad=前回のジャイロ角度rad+ジャイロrad/s*実行周期ms
ang_rad += gyr_rad*sample_time_s;
これでロボットを立てると正の角度が出るはずです。
積算した角度が±PIを超えると計算しづらいので±PIに補正しておきます。
角度rad = (角度rad> PI)? 角度rad-2*PI : (角度rad<-PI)? 角度rad+2*PI: 角度rad
この式は頻繁に使うので関数として用意しておきましょう。
float limit_pi(float ang_rad){
float value;
value = (ang_rad> PI)? ang_rad-2*PI :
(ang_rad<-PI)? ang_rad+2*PI : ang_rad;
return value;
}
ついでに180度バージョンも作っておきます。
float limit_180(float ang_deg){
float value;
value = (ang_deg> 180)? ang_deg-360 :
(ang_deg<-180)? ang_deg+360 : ang_deg;
return value;
}
これを使ってang_radを補正します。
ang_rad=limit_pi(ang_rad);
次に、逆三角関数を使って加速度からも角度を求めます。
asin、acos、atanのいずれでも角度を算出することはできますが、
360度どの位置でも角度を出すには標準関数のatan2を使います。
ang_acc=atan2(-acc_x,acc_z);
ここでジャイロから計算した角度と加速度から計算した角度を比較しておきます。
M5系の様にモニターが付いていればそのまま表示するのが簡単でしょう。
モニターが無い場合はシリアル通信などでPCへ転送します。
内部計算はrad,rad/s単位ですが、出力はdeg,deg/sで構いません。

およそ同じ値を示すはずです。
写真ではジャイロ角度「45.78 deg」加速度角度「43.31 deg」となっています。
同じような値にならない場合は使用する値や符号が間違っている可能性があるので確認してください。
静止状態で計算した2つの角度を比較します。

ゼロ点調整次第でもありますが水平状態等装置が安定していてもジャイロから計算した角度は少しずつ変化しているのが分かると思います。これに対して加速度から計算した角度はギザギザしているものの、平均値としては同じ角度を保っています。
続いて、装置を揺さぶった状態で比較してみます。
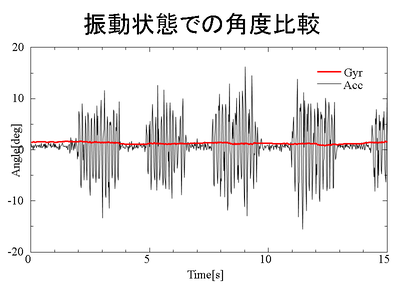
ジャイロから計算した角度は多少揺さぶっても安定しているのに対して、今度は加速度から計算した角度が暴れています。
そこで、ジャイロから計算した角度をベースとしつつ、加速度から計算した角度で補正を掛けます。
角度オフセット=加速度角度rad-現在のジャイロ角度rad
この角度差も±piに補正します
ang_dif=(ang_acc-ang_rad);
ang_dif=limit_pi(ang_dif);
※2023/01/26 変数名をang_subからang_difへ変更
現在のジャイロ角度rad+=角度オフセット*実行周期ms/1.0f
ang_rad+=ang_dif*sample_time_s/1.0f;
これでジャイロ角度と加速度角度の平均値に差が出ていると補正がかかります。
1.0fの部分で加速度による補正の強さが変わります。
1.0だと1秒で角度差が埋まるイメージです。
補正した角度と加速度から計算した角度を比較してみます。

静止時ではほぼ同じ角度になり、振動させたときも安定しています。
角度を変えると素早く反応します。
補正の強さは適宜調整してください。
これで角度計算ができました。
まずパルスを距離に変換します。
距離はメートル単位で扱う事にします。
パルスから距離への換算は
・エンコーダ軸の回転量 = エンコーダパルス数 / 1回転当たりのパルス数
・タイヤ軸の回転量 = エンコーダ軸の回転量 / エンコーダ軸・タイヤ軸ギヤ比
・移動距離 = タイヤ軸の回転量*タイヤ半径*2*PI
となります。
1回転当たりのパルス数
今回使用するEC10E1220505の仕様を見ると1回転のパルス数は12となっています。
マイコン側のカウントの方法によっても変わりますが、パルスを4逓倍でカウントした場合は1回転当たりにカウントされるパルス数は4倍の48パルスとなります。
ギヤ比
動力軸の回転としては
・モーター軸
・エンコーダ軸
・タイヤ軸
の3つがあり、それぞれがギアで連動して動きます。
シングルギヤボックスの38.2:1セッティングの場合モーター軸からタイヤ軸までは
ピニオンギヤ8T-クラウンギヤ34T/12T-2段ギヤ36T/12T-ファイナルギヤ36T
と繋がっています。
自分で計算してみると
モーター軸・タイヤ軸ギヤ比=1/8*34/12*36/12*36/1=38.25
と確認できます。
同様に114.7セッティングの場合は
ピニオンギヤ8T-クラウンギヤ34T/12T-2段ギヤ36T/12T-2段ギヤ36T/12T-ファイナルギヤ36T
となるので
モーター軸・タイヤ軸ギヤ比=1/8*34/12*36/12*36/12*36/1=114.75
と確認できます。
動力的にはモーター軸・タイヤ軸間のギヤ比が重要ですが、移動距離などの計算には
エンコーダ軸・タイヤ軸間のギヤ比が必要になります。
マウス用エンコーダを付けた例では38.2:1、114.7:1共にエンコーダはタイヤ軸の1段前の2段ギヤに接続したので、エンコーダ軸・タイヤ軸間のギヤ比は
エンコーダ軸・タイヤ軸ギヤ比=1/12*36/1=3
となります。
つまり、タイヤ軸の回転量はエンコーダ軸の回転量の1/3となります。
12.7:1セッティングの場合はタイヤ軸の先にエンコーダ軸があり
エンコーダ軸・タイヤ軸ギヤ比=1/36*12=1/3
となり、タイヤ軸はエンコーダ軸の3倍の回転量になっています。
タイヤの半径
これは素直に直径を半分にすればOKです。
タミヤ スポーツタイヤだと直径が56mm実測した直径が54mmなので半径は27mm→0.027mです。
以上よりパルス数から距離の換算式は
4逓倍で取得したパルス数を
pls_raw
とし、1回転当たりのパルス数、エンコーダ軸・タイヤ軸ギヤ比、タイヤ半径をそれぞれ
pls_rev = 48.0f;
gear_enc_tire = 1/12.0f*36.0f;
radi_tire = 0.027f;
とすると、現在の移動距離は
dis_now = pls_raw / pls_rev / gear_enc_tire * radi_tire * 2*PI;
となります。
求まった距離が正しいかタイヤを転がしながら地面を移動させて計算値を確認してください。
また、最初に定義した前と距離の増加方向が一致するか確認してください。
一致しない場合はパルスのABポートを入れ替えるかdis_now計算時に-1をかけて符号を変えてください。

100mmの前進で102mmとなったので良さそうです。
移動距離が求まったので速度を求めます。
移動速度m/s=(現在の距離-前回の距離)/実行周期ms
として計算します。
プログラム1周期分の実行終了時に現在の移動距離を前回の移動距離として記憶しておき
dis_old = dis_now;
差分から速度を計算します
spd_now = (dis_now / dis_old)/sample_time_s;
計算した速度はシリアル通信等で確認してください。
これでセンシングの準備ができました。
正逆回転用にPWM出力プログラムを設定し、モータードライバ、モーター電源、モーターを接続します。
出力比を-1~1で設定する変数を用意します。
out_rate=0;
出力には±1で出力上限を設けます。
out_rate=(out_rate>1)?1:(out_rate<-1)?-1:out_rate; //出力値保護
一旦PWM分解能を設定 ※1024段階の場合
out_pwm=out_rate*1023;
ABポートへの出力値設定(常時回生)
if(out_pwm>0){
out_A=1024;
out_B=1024-out_pwm;
}else if(out_pwm<0){
out_A=1024+out_pwm;
out_B=1024;
}else{
out_A=1024;
out_B=1024;
}
これでout_Aを正転用ポート、out_Bを逆転用ポートから出力すればout_rateでモーターの出力指示ができます。
ただ、ギヤの組み方やモーターの配線等で正転=前進となっているかは分かりません。
実際に出力して、正転=前進となっているか確認し、逆転している場合はモーターの配線変更または出力ポートの変更で正逆と前後進を一致させてください。
これでセンシングの準備が出来ました。
次回、主要パラメータを測定します。
マイコン等が搭載された側を表(上)とします。
前後
地面に寝かせた状態でタイヤのある側を後ろとします。
表裏と前後を決めれば左右が決まります。
角度
表面を上にして寝かせた状態を0度とします。
ここから立たせる側を正とします。
構造によりますが、立った状態でほぼ+90度となります。
角度を求める
倒立制御にはロボットの傾斜角度を高速で取得する必要になります。そこで、ジャイロ(角速度)と加速度から傾斜角度を計算します。
既存のライブラリーで手軽に済ますならMadgwickフィルターを使うのが良いでしょう。
今回はどんな環境でも実行できるようになるべく原理レベルからプログラムも自作します。
クォータニオン等を使って姿勢計算するのがベストですが、とりあえず1軸だけ計算しておけばOKです。
カルマンフィルタを使う方が良いとかありますが、通信式ジャイロで倒立制御を行う分にはそこまで気にする必要はありません。今回は簡易的な相補フィルタで対応します。
とりあえずジャイロと加速度の生値を取得します。
ジャイロの感度は1000deg/s以上、できれば2000deg/sに設定します。
感度の調整方法とデータの取得方法は使用するジャイロのマニュアルに従ってください。
ジャイロと加速度の生値(raw)は以下に格納するとします。
gyr_x_raw,gyr_y_raw,gyr_z_raw
acc_x,acc_y,acc_z
この時点でどの軸がどっちを向いているか確認しておいてください。
どの軸がどっちを向いているかはセンサを取り付けた向きで異なります。
M5StickCを使ったテスト用の構成の場合
水平状態で加速度Zがプラス
垂直状態で加速度Xがマイナス
水平から垂直に動かすとジャイロYがプラス
となりました。
以降はこれを基準に説明します。
ジャイロの値は静止状態で0が出力されてない事があるので、
起動数秒間の値を平均してゼロ点として使います。
平均化の例
gyr_x_zero = gyr_x_zero*0.99f + gyr_x_raw*0.01f;
gyr_y_zero = gyr_y_zero*0.99f + gyr_y_raw*0.01f;
gyr_z_zero = gyr_z_zero*0.99f + gyr_z_raw*0.01f;
この例では1周期ごとに1%ずつ値が更新されます。
私はジャイロの変動量を見て、静止状態が1秒以上続いたら平均値としています。
生値からゼロ点を引いて現在値とします。
取得したジャイロの値がdeg/s等の場合はrad/sへ換算しておきます。
また、回転方向の定義とジャイロの向きが一致するように補正します。
今回は起こすとジャイロYがプラスなので
gyr_rad = +(gyr_y_raw - gyr_y_zero)/180.0f*PI;
となります。
ゼロ点補正したジャイロの値を実行周期毎に積算(数値積分)すれば角度になります。
現在のジャイロ角度rad=前回のジャイロ角度rad+ジャイロrad/s*実行周期ms
ang_rad += gyr_rad*sample_time_s;
これでロボットを立てると正の角度が出るはずです。
積算した角度が±PIを超えると計算しづらいので±PIに補正しておきます。
角度rad = (角度rad> PI)? 角度rad-2*PI : (角度rad<-PI)? 角度rad+2*PI: 角度rad
この式は頻繁に使うので関数として用意しておきましょう。
float limit_pi(float ang_rad){
float value;
value = (ang_rad> PI)? ang_rad-2*PI :
(ang_rad<-PI)? ang_rad+2*PI : ang_rad;
return value;
}
ついでに180度バージョンも作っておきます。
float limit_180(float ang_deg){
float value;
value = (ang_deg> 180)? ang_deg-360 :
(ang_deg<-180)? ang_deg+360 : ang_deg;
return value;
}
これを使ってang_radを補正します。
ang_rad=limit_pi(ang_rad);
次に、逆三角関数を使って加速度からも角度を求めます。
asin、acos、atanのいずれでも角度を算出することはできますが、
360度どの位置でも角度を出すには標準関数のatan2を使います。
ang_acc=atan2(-acc_x,acc_z);
ここでジャイロから計算した角度と加速度から計算した角度を比較しておきます。
M5系の様にモニターが付いていればそのまま表示するのが簡単でしょう。
モニターが無い場合はシリアル通信などでPCへ転送します。
内部計算はrad,rad/s単位ですが、出力はdeg,deg/sで構いません。
およそ同じ値を示すはずです。
写真ではジャイロ角度「45.78 deg」加速度角度「43.31 deg」となっています。
同じような値にならない場合は使用する値や符号が間違っている可能性があるので確認してください。
静止状態で計算した2つの角度を比較します。
ゼロ点調整次第でもありますが水平状態等装置が安定していてもジャイロから計算した角度は少しずつ変化しているのが分かると思います。これに対して加速度から計算した角度はギザギザしているものの、平均値としては同じ角度を保っています。
続いて、装置を揺さぶった状態で比較してみます。
ジャイロから計算した角度は多少揺さぶっても安定しているのに対して、今度は加速度から計算した角度が暴れています。
そこで、ジャイロから計算した角度をベースとしつつ、加速度から計算した角度で補正を掛けます。
角度オフセット=加速度角度rad-現在のジャイロ角度rad
この角度差も±piに補正します
ang_dif=(ang_acc-ang_rad);
ang_dif=limit_pi(ang_dif);
※2023/01/26 変数名をang_subからang_difへ変更
現在のジャイロ角度rad+=角度オフセット*実行周期ms/1.0f
ang_rad+=ang_dif*sample_time_s/1.0f;
これでジャイロ角度と加速度角度の平均値に差が出ていると補正がかかります。
1.0fの部分で加速度による補正の強さが変わります。
1.0だと1秒で角度差が埋まるイメージです。
補正した角度と加速度から計算した角度を比較してみます。
静止時ではほぼ同じ角度になり、振動させたときも安定しています。
角度を変えると素早く反応します。
補正の強さは適宜調整してください。
これで角度計算ができました。
速度を求める
次に車両速度を計算しておきます。まずパルスを距離に変換します。
距離はメートル単位で扱う事にします。
パルスから距離への換算は
・エンコーダ軸の回転量 = エンコーダパルス数 / 1回転当たりのパルス数
・タイヤ軸の回転量 = エンコーダ軸の回転量 / エンコーダ軸・タイヤ軸ギヤ比
・移動距離 = タイヤ軸の回転量*タイヤ半径*2*PI
となります。
1回転当たりのパルス数
今回使用するEC10E1220505の仕様を見ると1回転のパルス数は12となっています。
マイコン側のカウントの方法によっても変わりますが、パルスを4逓倍でカウントした場合は1回転当たりにカウントされるパルス数は4倍の48パルスとなります。
ギヤ比
動力軸の回転としては
・モーター軸
・エンコーダ軸
・タイヤ軸
の3つがあり、それぞれがギアで連動して動きます。
シングルギヤボックスの38.2:1セッティングの場合モーター軸からタイヤ軸までは
ピニオンギヤ8T-クラウンギヤ34T/12T-2段ギヤ36T/12T-ファイナルギヤ36T
と繋がっています。
自分で計算してみると
モーター軸・タイヤ軸ギヤ比=1/8*34/12*36/12*36/1=38.25
と確認できます。
同様に114.7セッティングの場合は
ピニオンギヤ8T-クラウンギヤ34T/12T-2段ギヤ36T/12T-2段ギヤ36T/12T-ファイナルギヤ36T
となるので
モーター軸・タイヤ軸ギヤ比=1/8*34/12*36/12*36/12*36/1=114.75
と確認できます。
動力的にはモーター軸・タイヤ軸間のギヤ比が重要ですが、移動距離などの計算には
エンコーダ軸・タイヤ軸間のギヤ比が必要になります。
マウス用エンコーダを付けた例では38.2:1、114.7:1共にエンコーダはタイヤ軸の1段前の2段ギヤに接続したので、エンコーダ軸・タイヤ軸間のギヤ比は
エンコーダ軸・タイヤ軸ギヤ比=1/12*36/1=3
となります。
つまり、タイヤ軸の回転量はエンコーダ軸の回転量の1/3となります。
12.7:1セッティングの場合はタイヤ軸の先にエンコーダ軸があり
エンコーダ軸・タイヤ軸ギヤ比=1/36*12=1/3
となり、タイヤ軸はエンコーダ軸の3倍の回転量になっています。
タイヤの半径
これは素直に直径を半分にすればOKです。
タミヤ スポーツタイヤだと直径が56mm実測した直径が54mmなので半径は27mm→0.027mです。
以上よりパルス数から距離の換算式は
4逓倍で取得したパルス数を
pls_raw
とし、1回転当たりのパルス数、エンコーダ軸・タイヤ軸ギヤ比、タイヤ半径をそれぞれ
pls_rev = 48.0f;
gear_enc_tire = 1/12.0f*36.0f;
radi_tire = 0.027f;
とすると、現在の移動距離は
dis_now = pls_raw / pls_rev / gear_enc_tire * radi_tire * 2*PI;
となります。
求まった距離が正しいかタイヤを転がしながら地面を移動させて計算値を確認してください。
また、最初に定義した前と距離の増加方向が一致するか確認してください。
一致しない場合はパルスのABポートを入れ替えるかdis_now計算時に-1をかけて符号を変えてください。
100mmの前進で102mmとなったので良さそうです。
移動距離が求まったので速度を求めます。
移動速度m/s=(現在の距離-前回の距離)/実行周期ms
として計算します。
プログラム1周期分の実行終了時に現在の移動距離を前回の移動距離として記憶しておき
dis_old = dis_now;
差分から速度を計算します
spd_now = (dis_now / dis_old)/sample_time_s;
計算した速度はシリアル通信等で確認してください。
これでセンシングの準備ができました。
モーターの回転方向
定義とモーターの回転方向を一致させておきます。正逆回転用にPWM出力プログラムを設定し、モータードライバ、モーター電源、モーターを接続します。
出力比を-1~1で設定する変数を用意します。
out_rate=0;
出力には±1で出力上限を設けます。
out_rate=(out_rate>1)?1:(out_rate<-1)?-1:out_rate; //出力値保護
一旦PWM分解能を設定 ※1024段階の場合
out_pwm=out_rate*1023;
ABポートへの出力値設定(常時回生)
if(out_pwm>0){
out_A=1024;
out_B=1024-out_pwm;
}else if(out_pwm<0){
out_A=1024+out_pwm;
out_B=1024;
}else{
out_A=1024;
out_B=1024;
}
これでout_Aを正転用ポート、out_Bを逆転用ポートから出力すればout_rateでモーターの出力指示ができます。
ただ、ギヤの組み方やモーターの配線等で正転=前進となっているかは分かりません。
実際に出力して、正転=前進となっているか確認し、逆転している場合はモーターの配線変更または出力ポートの変更で正逆と前後進を一致させてください。
これでセンシングの準備が出来ました。
次回、主要パラメータを測定します。
PR
コメント
プロフィール
カテゴリー
最新記事
(2025/11/17)
(2025/10/20)
(2025/10/05)
(2025/10/01)
(2025/09/30)
最新コメント
[2023/02/25 NONAME]
[2023/02/25 ぼんどF]
[2023/02/24 NONAME]
[2023/02/24 ぼんどF]
[2023/02/21 NONAME]
